天文上有一种重要的测距手段，叫作视差法，而在我们日常生活中可以用拇指测量法来简单估算距离
首先是视差法，在新概念物理教程 力学（第二版）p15提到了视差法。该方法如下图所示
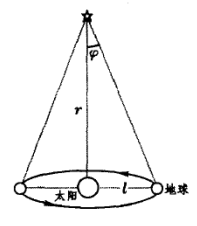
值得一提的是，我认为本书中有些地方表达的不清楚，如公式，文中描述为r=l/φ，可学过三角函数的应该知道，在该直角三角形中r=l/tanφ。此外，本书中表达视差法的时候提到”若视线与基线垂直......“若真垂直的话不应该是：
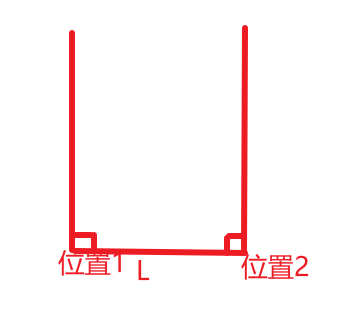
如此，怎么可能在不同位置观测同一天体？
视差法一般用于天体观测，基线l可以通过不同位置来控制，是已知量。φ可通过仪器测量。因此利用公式可以测得一些天体的距离。但局限性的是，该方法受限于基线，基线越长，能测的距离就越远。而我们在地球上，以半径为基线，可以测得地月，地日的距离。或者我们以地球公转半径为基线，此时基线长度就很大，可以向更大尺度的宇宙进发。
拇指测距法，该方法是利用相似三角形原理。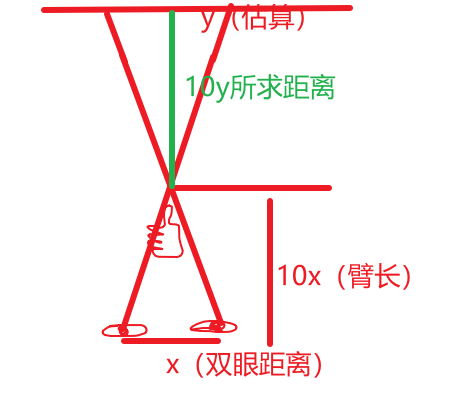
一般臂长是双眼距离的10倍，自己可以测量一下看看，姑且先按10倍来算，然后分别闭上左右眼看大拇指所在的远处的间距，估算该间距，有人说，如果能估算这个距离我不如直接估算目标和我的距离，但是大拇指远处的距离一般不长，或根据生活经验能够轻松估算，比如，远处有个楼，分别闭上左右眼看到拇指在那个楼的位置如图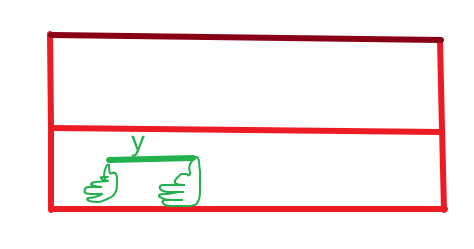
一般来说，楼层高是3米而拇指所处的位置和楼层高差不多，也就是估算为3m，那根据相似三角形，该楼距离为我也就是约30m。
估算3m和30m显然误差不同，3m更容易根据周围事物进行估算。这就是拇指测距。
评论0
暂时没有评论